A Simple Way to Find Turning points for a Trajectory with Python
Using Ramer-Douglas-Peucker algorithm (or RDP) that provides piecewise approximations, construct an approximated trajectory and find "valuable" turning points.
A trajectory is the path that a moving object follows through space as a function of time. Usually, we work with its discrete representation by calculating space positions with some interval.
For simplicity, let's consider only 2-dimensional space and ignore possible changes in Z coordinate. Therefore, our trajectory is a time series of data points (x, y) that represent position on a plane XY and have been calculated with some time interval.
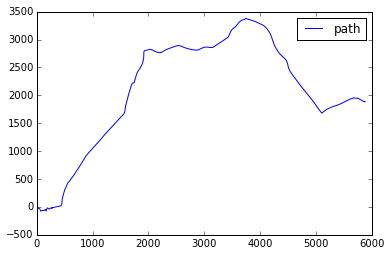
A turning point is just a changes in direction. Such points are valuable features for the trajectory analysis because they can define trajectories in a space (imaging you want to explain a path to someone, then you usually describe it in such turning points: "turn left, go 20 meters and turn right, go straight until you reach Starbucks, then turn right again.").
It's quite easy to find such turning points for humans on a plot, but a bit more tricky to do that automatically. A human brain can also quite fast detect valuable turning points when change in direction is significant (e.g. turning to another street in contrast to changing just a traffic lane).
In order to let machine make such analysis we need build a simple approximation to our trajectory curve where we can highlight such fractures. The best choice for this is Ramer-Douglas-Peucker algorithm (or RDP) that gives us a piecewise approximation to our trajectory curve where every fracture could be treated as a turning point.
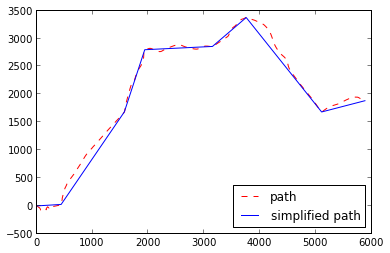
Trajectory can have many small noisy turns (e.g. due to calculation errors or just by representing a traffic lane change). Same as our brain do that, we want machine to filter them out too. As one of ways to do so, we can consider as a "valuable" only such significant turn whose angle is bigger than some minimal value (for instance, we have selected `\frac(\pi)(5)`, but you might find another value for your use case and data).
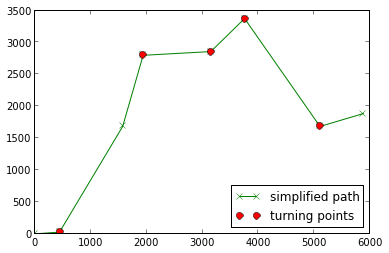
In the code below we use rpd 0.6 - pure Python implementation of the Ramer-Douglas-Peucker algorithm, and build simplified (or approximated) trajectory and compare it to the original curve.
Read More
- Ramer-Douglas-Peucker algorithm (RDP) is an algorithm for reducing the number of points in a curve that is approximated by a series of points.
